Kann man Mathematik mit Hilfe von Schach lernen? Xenia Bayer entführt die Hörer ihres Schachpodcasts für Kinder in die Welt der Zahlen und geometrischen Formen. Sie überlegt, wie Schach auf einem zylindrischen Brett aussehen könnte. Sie zerschneidet ein Schachbrett, und sie zeigt auf, wie man in 4 Zügen Matt setzt, wenn der Gegner alle Züge spiegelbildlich wiederholt. Am Ende hat sie auch noch eine Weisheit von Konfuzius parat.
Viel Vergnügen bei dieser Folge über Schach und Mathematik!
EPISODENLINKS:
♕ TSV München Solln e.V. – YouTube
SCHACHAKADEMIE:

Episodenskript
Hallo liebe Zuhörer,
ich heiße Xenia Bayer und das ist mein Podcast „Schach für Kinder“! Die 27. Folge: „Kann man Mathematik mithilfe von Schach lernen?“
Als ich 8 Jahre alt war, entdeckte ich für mich das Schachspiel, welches mich noch immer fasziniert. Später, als ich an der Uni mit der Hohen Mathematik beschäftigt war, interessierte ich mich für mathematische Rätsel und Knobeleien und habe festgestellt, dass Schach und Mathematik viele Gemeinsamkeiten haben.
In die faszinierende Welt der Mathematik auf dem Schachbrett führe ich jetzt auch Schachkinder aus unserem Verein. Rätsel, Puzzles, interessante und ungewöhnliche Schachaufgaben: All das bietet der Kurs „Mathematik auf dem Schachbrett“, den ich regelmäßig in unserem Verein für Kinder von 6 bis 12 Jahren organisiere.
Auch Euch, liebe Zuhörer, möchte ich diese Welt nicht vorenthalten.
Die Kunst der Zahlen
Arithmetik heißt die Kunst der Zahlen. Um das Zählen und das Rechnen zu vereinfachen, haben die Mathematiker die Arithmetik entwickelt.
Zählen und Rechnen kann man leicht mit Schachfiguren lernen. Jede Schachfigur hat einen Wert: der Springer z.B. ist so stark wie drei Bauern, der Turm wie die 5 Bauern und die Dame ist sogar 9 Bauern wert. Im Schach unterscheidet man zwischen Leichtfiguren (Läufer und Springer) und Schwerfiguren (Turm und Dame).
Wenn du eine Figur schlagen möchtest, vergleiche die Punktezahl deiner Figur und der Figur, die du schlägst. Ist die Punktzahl deiner Figur höher, dann ist der Abtausch schlecht!
Gerade und ungerade Zahlen
Der Springer hat eine besondere Eigenschaft. Er wechselt bei jedem Zug die Feldfarbe. Diese Eigenschaft kann uns helfen, um zwischen geraden und ungeraden Zahlen zu unterscheiden. Ich stelle den Springer auf das Schachbrett. Der Springer reist vom Feld a8 über das ganze Schachbrett und kehrt nach a8 zurück. Unsere Aufgabe ist es herauszufinden, ob er eine gerade oder ungerade Anzahl von Zügen gemacht hat. Habt Ihr eine Idee wie man es schnell lösen kann?

Bei seinem ersten Zug landet der Springer auf einem schwarzen Feld, da das Feld a8 eine weiße Farbe hat. Bei dem zweiten Zug ist der Springer auf einem weißen Feld. Die Zahl 1 ist eine ungerade Zahl und in unserer
Aufgabe bekommt sie die Farbe Schwarz. Die Zahl 2 ist eine gerade Zahl und ist bei uns jetzt weiß. Der Springer startet vom weißen Feld und kehrt auf das weiße Feld zurück. Kennt ihr schon die Antwort?
Richtig! Von weiß auf weiß hat der Springer eine gerade Zahl von Zügen gemacht! Um die Aufgabe zu lösen braucht man keine Züge zu zählen, man muss sich nur die Farbe des Feldes merken.
Die Schachfiguren können zaubern. Ihr glaubt das nicht? Aber es ist wahr! Wenn ein Bauer ans andere Brettende (die 1. Reihe für Schwarz bzw. die 8.Reihe für Weiß) gelangt, wandelt er sich in eine beliebige Figur um (z.B. in eine Dame oder Turm, nur nicht in einen König).
Das zylindrische Schachbrett und die unendlichkeit
Das Schachbrett selbst kann sich auch verwandeln, z. B. in ein Kreis-Schachbrett oder in ein Zylinder-Schachbrett.
Wenn man die linke Brettseite mit der rechten Brettseite zusammenklebt, hat man ein vertikales Zylinderschachbrett. Die untere Seite bildet zusammen mit der oberen Seite ein horizontales Schachbrett. Schach auf dem Zylinderschachbrett wird so gespielt:
Wenn eine Figur einen Rand des Brettes erreicht, erscheint sie am anderen Rand wieder. Und jetzt die Aufgabe:
Die Stellung auf dem normalen Brett: Weiß: Ke2, Bauer g7; Schwarz: Kc4 Kann Schwarz sich retten? Auf dem normalen Brett wird der Bauer in eine Dame umgewandelt und Schwarz verliert.
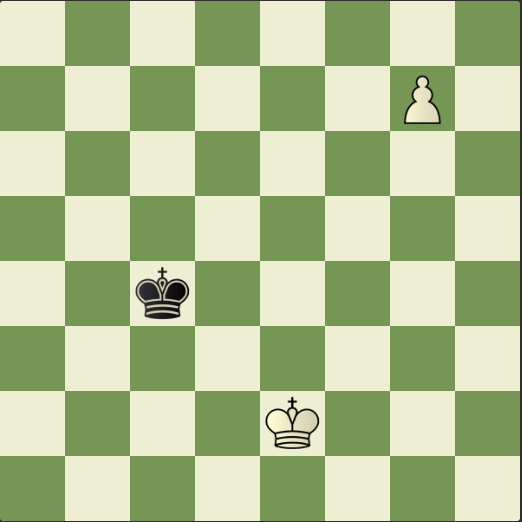
Schwarz ist aber kreativ. Er macht aus dem Schachbrett ein horizontales Zylinderschachbrett, und der weiße Bauer kann nicht mehr umgewandelt werden. Der Bauer wird auf der g-Linie unendlich lang marschieren: wenn er einen Rand des Brettes erreicht, erscheint er am anderen Rand wieder. Diese Aufgabe gibt uns auch die Antwort auf die interessante Frage „Was ist Unendlichkeit?“.
Den geometrischen Begriff „Symmetrie“ kann man mit der Grundstellung auf dem Schachbrett erklären. Schwarz und Weiß haben am Anfang der Partie symmetrische Stellungen. Die weißen Figuren spiegeln sich in Schwarz und die Schwarzen in Weiß.
WERBUNG:
Schachgeflüster Leitfaden für Einsteiger und Eltern, jetzt zum Preis von 9,90 € beim Schachdepot

Das Symmetriematt
Amerikas berühmtester Spiele- und Rätselerfinder Samuel Loyd hat ein Symmetriematt gefunden. Eines Tages in dem Schachklub, wo Loyd gewöhnlich Schach spielte, kam ein junger Mann, der behauptete, herausgefunden zu haben, wie man mit den schwarzen Figuren nie verliert. Als man ihn fragte, auf welche Weise es möglich ist, antwortete der junge Mann: „Ganz einfach! Man muss die Züge des Gegners wiederholen!“
Samuel Loyd forderte den Erfinder zu einer Partie heraus und setzte ihn in 4 Zügen matt:
1.d4 d5 2.Dd3 Dd6 3.Dh3 Dh6 4.Dc8#
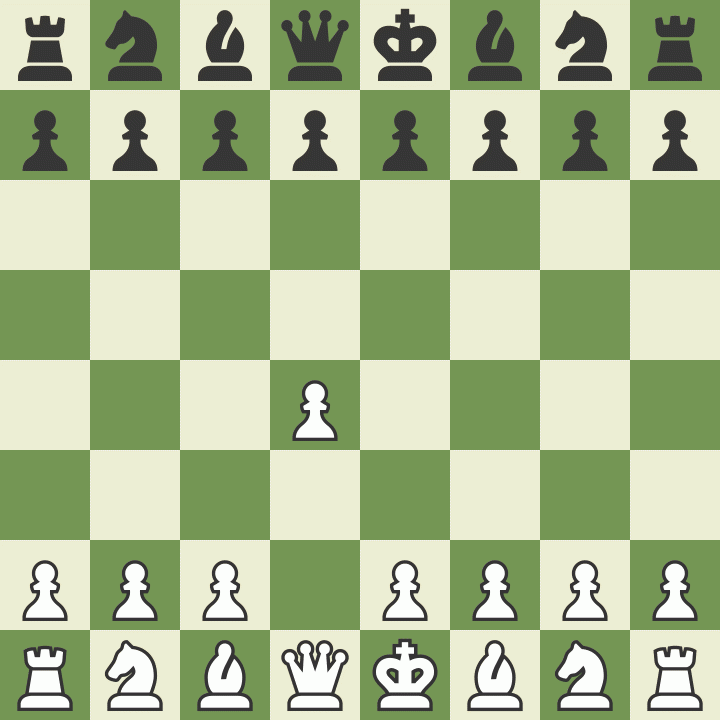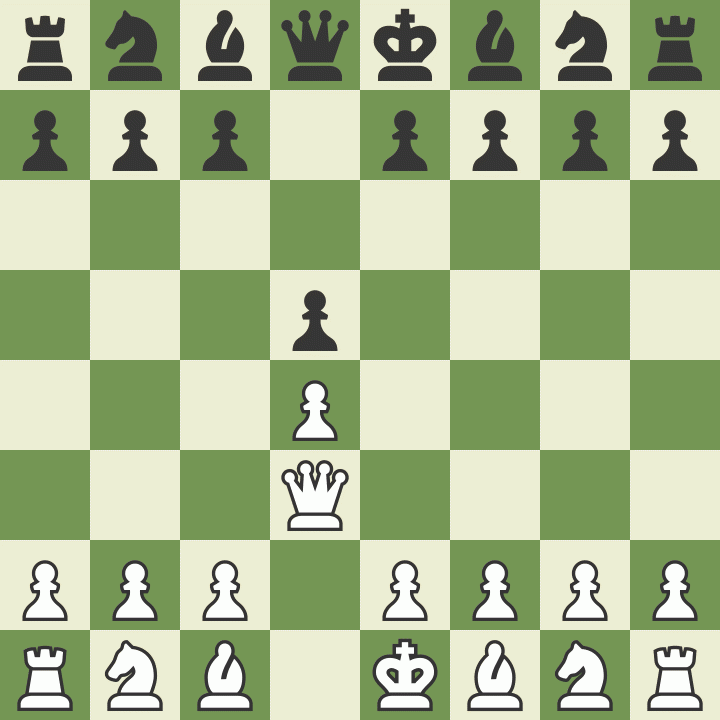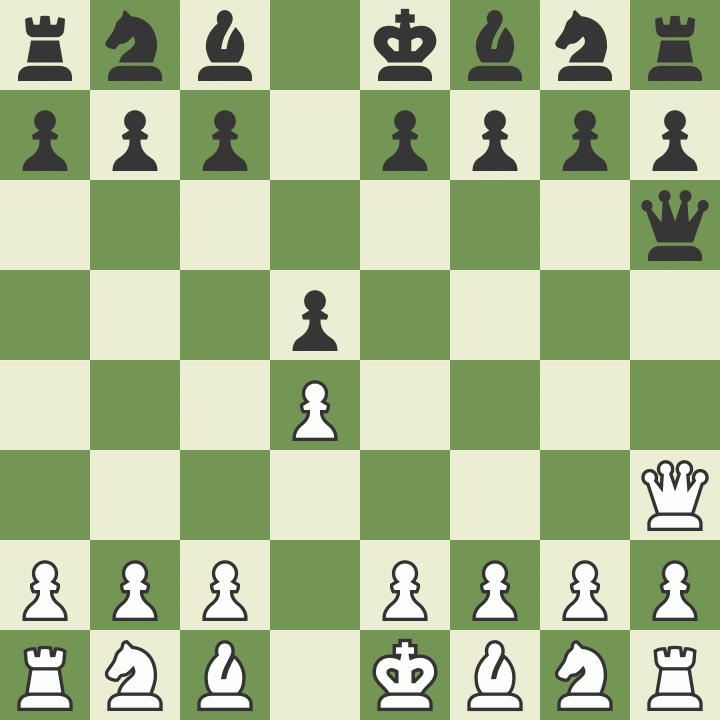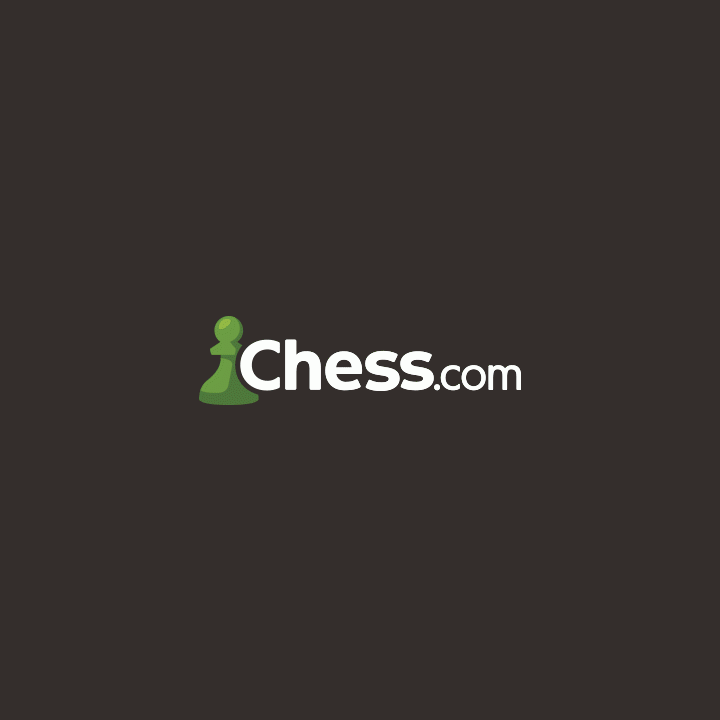
Die Zweierpotenz
Noch eine Aufgabe zur Geometrie: Das Schachbrett wird in 64 Teile geschnitten. Findet die kleinste Anzahl an Schnitten.
Und, wie viele Schnitte habt ihr gebraucht? Die richtige Antwort ist 6!
Wir schneiden das Schachbrett in der Mitte in zwei Teile. Diese Teile werden aufeinandergelegt und wieder geschnitten. Aus 2 Teilen haben wir jetzt 4 bekommen. Diese legen wir alle aufeinander und schneiden wieder. Das machen wir dann mit 8 Teilen, 16 Teilen und 32 Teilen. Bei jedem Schnitt haben wir das Doppelte bekommen.
Aus der Mathematik wissen wir, dass 2 hoch 6 gleich 64 ist. So können wir auch mathematisch beweisen, dass man für 64 Teile nur 6 Schnitte braucht.
Meine heutige Folge möchte ich mit einem Zitat des chinesischen Philosophen Konfuzius beenden:
Was du mir sagst, das vergesse ich.
Was du mir zeigst, daran erinnere ich mich.
Was du mich tun lässt, das verstehe ich
Konfuzius
Dank mathematischen Experimenten auf dem Schachbrett wird Mathematik kein langweiliges Schulfach mehr!
Bis zum nächsten Mal! Eure Xenia Bayer

